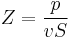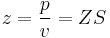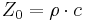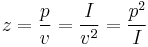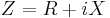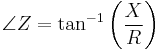Acoustic impedance
| Sound measurements |
|---|
| Sound pressure p, SPL |
| Particle velocity v, SVL |
| Particle displacement ξ |
| Sound intensity I, SIL |
| Sound power Pac |
| Sound power level SWL |
| Sound energy |
| Sound energy density E |
| Sound energy flux q |
| Acoustic impedance Z |
| Speed of sound c |
| Audio frequency AF |
The acoustic impedance at a particular frequency indicates how much sound pressure is generated by a given air vibration at that frequency. The acoustic impedance Z (or sound impedance) is frequency (f) dependent and is very useful, for example, for describing the behaviour of musical wind instruments. Mathematically, it is the sound pressure p divided by the particle velocity v and the surface area S, through which an acoustic wave of frequency f propagates. If the impedance is calculated for a range of excitation frequencies the result is an impedance curve. Planar, single-frequency traveling waves have acoustic impedance equal to the characteristic impedance divided by the surface area, where the characteristic impedance is the product of longitudinal wave velocity and density of the medium. Acoustic impedance can be expressed in either its constituent units (pressure per velocity per area) or in rayls per square meter.
Note that sometimes vS is referred to as the volume velocity.
The specific acoustic impedance z is the ratio of sound pressure p to particle velocity v at a single frequency and is expressed in rayls. Therefore
Distinction has to be made between:
- the characteristic acoustic impedance
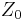of a medium, usually air (compare with characteristic impedance in transmission lines). - the impedance
of an acoustic component, like a wave conductor, a resonance chamber, a muffler or an organ pipe.
Contents |
Characteristic acoustic impedance
Characteristic acoustic impedance of air vs temperature at atmospheric pressure
| Temperature | Speed of sound | Density of air | Acoustic impedance |
|---|---|---|---|
 in °C |
c in m·s−1 | ρ in kg·m−3 | Z in N·s·m−3 |
| +35 | 351.96 | 1.1455 | 403.2 |
| +30 | 349.08 | 1.1644 | 406.5 |
| +25 | 346.18 | 1.1839 | 409.4 |
| +20 | 343.26 | 1.2041 | 413.3 |
| +15 | 340.31 | 1.2250 | 416.9 |
| +10 | 337.33 | 1.2466 | 420.5 |
| +5 | 334.33 | 1.2690 | 424.3 |
| ±0 | 331.30 | 1.2920 | 428.0 |
| -5 | 328.24 | 1.3163 | 432.1 |
| -10 | 325.16 | 1.3413 | 436.1 |
| -15 | 322.04 | 1.3673 | 440.3 |
| -20 | 318.89 | 1.3943 | 444.6 |
| -25 | 315.72 | 1.4224 | 449.1 |
The characteristic impedance of a medium, such as air, rock or water is a material property:
where
- Z0 is the characteristic acoustic impedance ([M·L–2·T−1]; N·s/m3 or Pa·s/m)
- ρ is the density of the medium ([M·L−3]; kg/m3), and
- c is the longitudinal wave speed or sound speed ([L·T−1]; m/s)
The characteristic impedance of air at room temperature is about 420 Pa·s/m. By comparison the sound speed and density of water are much higher, resulting in an impedance of 1.5 MPa·s/m, about 3400 times higher. This differences leads to important differences between room acoustics or atmospheric acoustics on the one hand, and underwater acoustics on the other.
Specific impedance of acoustic components
The specific acoustic impedance z of an acoustic component (in N·s/m3) is the ratio of sound pressure p to particle velocity v at its connection point:
where
- p is the sound pressure (N/m² or Pa),
- v is the particle velocity (m/s), and
- I is the sound intensity (W/m²)
Complex impedance
In general, a phase relation exists between the pressure and the particle velocity. The complex impedance is defined as
where
- R is the resistive part, and
- X is the reactive part of the impedance
The resistive part represents the various loss mechanisms an acoustic wave experiences such as random thermal motion. For the case of propagation through a duct, wall vibrations and viscous forces at the air/wall interface (boundary layer) can also have a significant effect, especially at high frequencies for the latter. For resistive effects, energy is removed from the wave and converted into other forms. This energy is said to be 'lost from the system'.
The reactive part represents the ability of air to store the kinetic energy of the wave as potential energy since air is a compressible medium. It does so by compression and rarefaction. The electrical analogy for this is the capacitor's ability to store and dump electric charge, hence storing and releasing energy in the electric field between the capacitor plates. For reactive effects, energy is not lost from the system but converted between kinetic and potential forms.
The phase of the impedance is then given by
